Square Roots and Negative Numbers
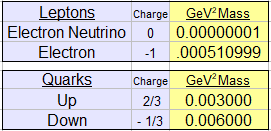
Fermion generation 1 GeV/C² mass observables
Analysis of generation 1 fermion masses utilizing the geometric mean yields a highly graphic representation of generation 1 quarks and leptons.
They reveal relationships among all generation 1 fermion particles, beta decay and atomic structure.
METHOD
GEOMETRIC REPRESENTATION OF GENERATION 1 FERMIONS
BETA DECAY BY GEOMETRIC MEAN
HYDROGEN BY GEOMETRIC MEAN
CONCLUSIONS
_____________________________________________________________
METHOD
Square Roots and Negative Numbers
Fermion generation 1 GeV/C² mass observables

Square roots for negative numbers are unachievable, so we normalize all generation 1 fermion observable mass values to positive numbers.
Below, all mass values of the main diagonal in blue are actual observable fermion GeV/C² masses.
The green values of top row and first columns are the square roots of each respective fermion mass.

* Source of GeV/C² or main diagonal masses: Lawrence Livermore Laboratories, March 2011
We take all lepton and fermion mass values in gigavolts and shift 9 places to left (decavolts) where the electron neutrino (or speed of light) is 1.
The green section is the elementary particles in the usual GeV/C² .
The blue section is shifted 9 places (decavolts) where electron neutrino is 1.
The yellow section are square roots.
The red section is shifted 9 places to the right, or the actual square root in GeV/C²

Electron Neutrino = Speed of Light = 1
Electron neutrino speed did not detect statistically significant deviations from the speed of light.
* Source: https://en.wikipedia.org/wiki/Measurements_of_neutrino_speed, June 2022
_________________________________________________________________________________________________________________
GEOMETRIC REPRESENTATION OF GENERATION 1 FERMIONS
Let x = the square root of Electron or .0000022605 GeV/C²
Utilizing the table above, we take a peek at what is happening between all row and column vectors.

x = √Electron
x + √(x + x) = √Up Quark
x + x + √(x + x) = √Down Quark
Fermion masses defined geometrically give a representation as components of a right triangle (!).
The Down Quark algorithm x + x + √(x + x) is equivalent to adding the 3 sides of a right triangle or calculating the perimeter of the right triangle above.
The Up Quark algorithm x + √(x + x) is equivalent to a right triangle missing either of the 2 equal sides or legs. +-.00094%.
_________________________________________________________________________________________________________________
BETA DECAY BY GEOMETRIC MEAN
Figure 4.1 - Beta Decay
N -> P + E + eV
The GeV/C² of the Electron Neutrino (.00000001) + Electron (.0000022605) + Up quark (.0000054772) = Down Quark (.0000077459) +-.00033%
Beta decay or Neutron -> Proton + Electron + Anti-Electron Neutrino is represented exactly by any of the following equations:
Anti-Electron Neutrino + Electron + Proton <- Neutron
or
Anti-Electron Neutrino + Electron + Up Quark <- Down Quark
or
√Anti-Electron Neutrino + √Electron + √Up = √Down
or
.00000001 + .0000022605 + .0000054772 = .0000077459
(top row or first column of matrix below)
or
Beta Decay: Arithmetic vs. Geometric Mean
Mass values for the individual particles involved in beta decay do not add up when using any conventional fermion chart.
When computing with the arithmetic mean, the down quark (.00600 GeV/C² ) does not equal the anti-electron neutrino + electron + up quark (.00951101 GeV/C² ).
But, when computing with the same values utilizing geometric mean, the down quark is equal to an up quark plus an electron plus an anti electron neutrino.
Analysis of Generation 1 and Beta Decay utilizing arithmetic versus geometric mean

When analyzed by arithmetic mean, the Up quark times 2 equals a Down quark.
When computing utilizing the geometric mean, the Up quark + Electron + Electron Neutrino times the square root of 2 equals a Down quark.
Fermion Generation 1 and Beta Decay: Arithmetic versus Geometric mean
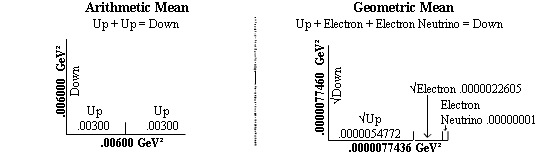
Up Quark * 2 = Down Quark (Arithmetic Mean)
√Up Quark + √Electron + Electron Neutrino = √Down Quark (Geometric Mean)
While the electron neutrino, electron and up quark combined equal a down quark geometrically (+-.9994%), this symmetry is not exhibited using the arithmetic mean.
_________________________________________________________________________________________________________________
HYDROGEN BY GEOMETRIC MEAN
Below, a chart of the hydrogen atom using geometrically defined generation 1 objects: the square roots of the electron, up quark and down quark.
We add the up and down quark components of the proton (.00002096 GeV/C² ), and compare with the up and down quark components of the neutron plus electron (.00002097 GeV/C² ).
This particular bilateral symmetry entails both quarks and leptons. This symmetry is not apparent utilizing the usual arithmetic mean.
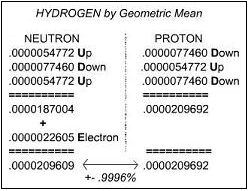
In the figure below, we add the geometrically defined mass components of the neutron and compare with the components of the proton plus electron.
_________________________________________________________________________________________________________________
CONCLUSIONS

Utilizing geometric representations of the first generation fermions we construct multiple fermion generation 1 objects including beta decay, pions and hydrogen.
Geometrically defined bilateral symmetries of fermion generation 1 objects
Each tier of the diagram above depicts a geometrically defined object derived from observable fermion masses.
Each object gets larger in mass as we go down the rows.
The graphic also entails how all these generation 1 objects are different from each other while being composed of the same fermion generation 1 elementary particles.
These representations are not possible using the arithmetic mean for elementary particles, but utilize the geometric mean.